9  Single-cell lineage tracing

9.1 Why are we interested in learning temporal dynamics?

Studying how cells change over time provides critical insight into the sequence of events driving biological processes. By observing changes in cell populations across multiple time points, researchers can pinpoint when specific transitions or bifurcations occur. Such temporal information reveals which factors influence a cell’s fate and how quickly new traits emerge.

Moreover, understanding temporal dynamics can help us develop better interventions. If we can identify the earliest signs of disease or undesirable changes in cells, then targeted therapies can be designed to prevent or slow progression. Such strategies are especially powerful for complex, multi-stage diseases where later intervention might be less effective.

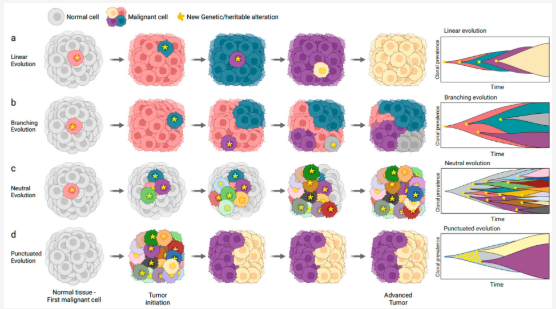
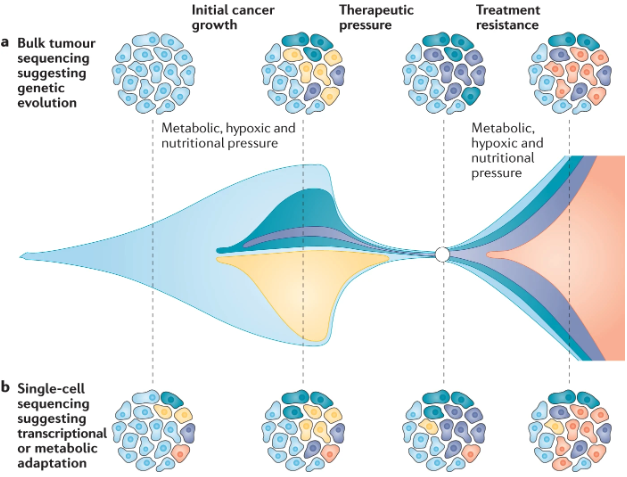
  • Cancer subclone evolution: Tumors consist of various subclones that compete and evolve. Observing which subclones become dominant over time helps illuminate how certain cells acquire and propagate new mutations, sometimes conferring resistance to treatments. See Figure 9.1 and Figure 9.2.
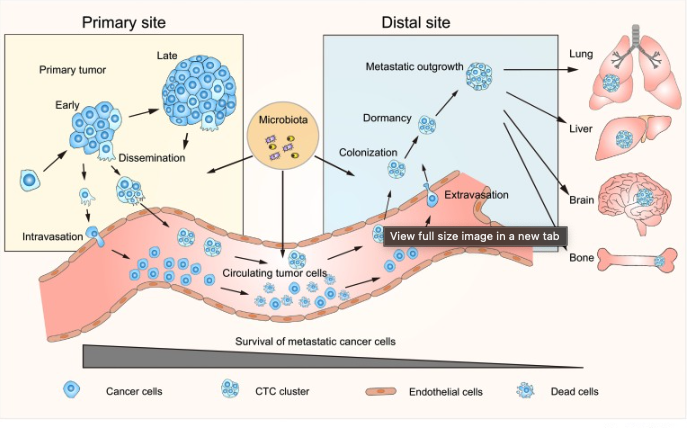
Figure 9.1: (Top) From (ashouri2023decoding?).
Figure 9.2: (Bottom) From (marine2020non?).
  • Cancer metastasis: Cells that detach from the primary tumor site and successfully colonize new tissues undergo significant genetic and phenotypic changes. Understanding these changes in temporal sequence highlights the adaptations needed for invasion and survival in distant environments. See Figure 9.3.
Figure 9.3: From (fu2023emerging?).
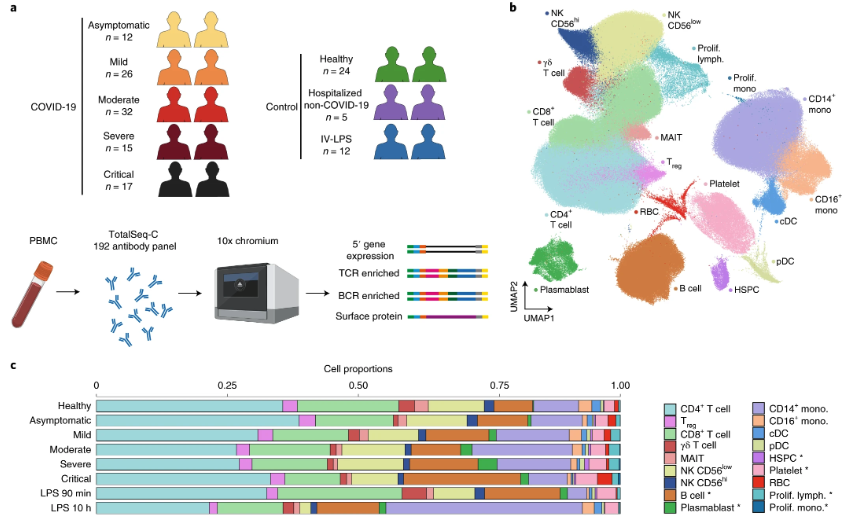
  • Disease progression: Many diseases advance in stages, even beyond cancer, with cells accumulating subtle changes that eventually manifest as severe pathologies. Timing the acquisition of these changes reveals how early molecular events cascade into full-blown disease. See Figure 9.4 for an example of this investigated in COVID.
Figure 9.4: From (stephenson2021single?). You can see that at different stages of COVID, there is a slightly different proportion of cell types that constitute the immune system.
  • Embryonic/organ development and cell fate: During embryonic development, cells undergo a series of tightly regulated fate decisions that determine their final identity. These decisions are influenced by both intrinsic genetic programs and extrinsic signaling cues from the surrounding environment. Understanding the temporal dynamics of these transitions allows researchers to uncover the molecular mechanisms guiding differentiation and tissue formation. By tracking how cells commit to specific lineages, we gain insight into how organs form or how “cells make decisions”. See Figure 9.5.
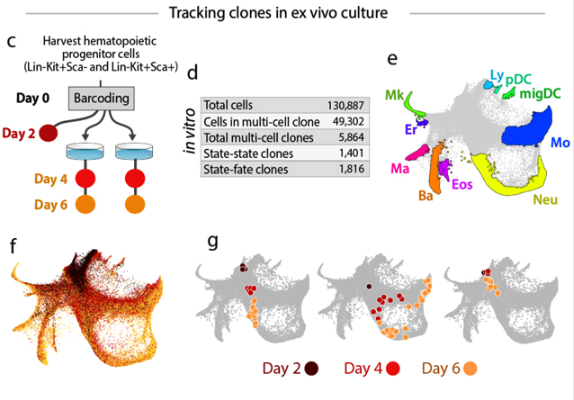
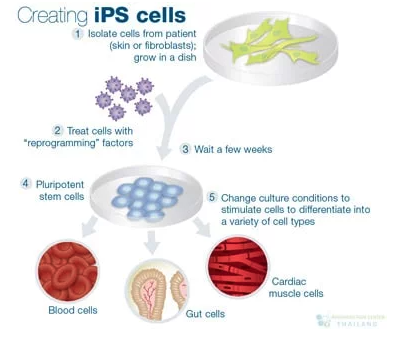
Figure 9.5: From (weinreb2020lineage?). This dataset is recorded longitudinally (i.e., cells were sequenced at Day 2, 4, and 6.) What’s shown here are cells known to be in different lineages, but certain lineages don’t differentiate by Day 6, differentiate into multiple cell types, or differentiate only into one cell type.
  • Stem cell research: Stem cells differentiate into specialized cell types following a tightly regulated timeline. Tracking these progressions uncovers the signals that guide each step and may inform regenerative medicine strategies for repairing damaged tissues. See Figure 9.6.